ブーツトラップ法で95%信頼区間を推定
私はこの時、認知症になってしまった祖母の介護を手伝っていたものの、結局次の研究職を見つけられないまま、無職の状態で論文をまとめていたことになるわけです。無職ではありますが、せっかくこのような、言ってみれば時間に余裕があるときに、これまでと同じことをしていては自分自身成長がないような気がしたので、これも新たな分析の手法を身につける良い機会だろうと考えました。以前発表した論文では(Miyo and Charlesworth, 2004; Miyo et al., 2006)、抵抗性と感受性の遺伝子型に関する集団の遷移軌道について、ブーツトラップ法を用いて個体数の比の標準誤差を推定しましたが、今回は標準誤差だけでなく、ブーツトラップ・レプリケーションの分布に基づいて、95%信頼区間を設定することにしました。以前にも述べましたが、標準誤差の推定の場合であれば、それほど多くのレプリケーションは必要ではないのですが、ブーツトラップ・レプリケーションの分布に基づいて95%信頼区間を設定する場合には、分布の端の値を用いることになるので、標準誤差の推定の場合よりも多くのレプリケーションが必要であり、通常は500から1000のレプリケーションが目安であるということでした(Efron and Tibshirani, 1993)。職に就かずにただ遊んでいるのではなく、少しは成長していることを示さなければならないと思ったので、手間と時間はかかりましたが、ブーツトラップ法を使って、標準誤差だけでなく95%信頼区間を設定することにしました。
ブーツトラップ法という統計的な手法は、イギリスで勉強していた時に、エジンバラでお世話になっていた先生からこの手法を使ってみたらどうかと紹介していただき、自分も教科書などを読んで勉強してきました。エジンバラでお世話になっていた教授であれば、ご自身でコンピューターのプログラムを書くことができ、分析もほんの一瞬で終わっていただろうと思いますが、私もエジンバラでコンピューター言語を少しかじったとはいえ、いろいろとわからないことがあったので、マイクロソフト社のExcelという表計算ソフトを使って、ひとつひとつのブーツトラップ・レプリケーションを、いちいち確認しながら、1つずつレプを増やしていくことにしました。以前の論文では、170レプリケーションでしたが、それでも数か月かかったことになりますし、エジンバラでお世話になっていた先生も、恐らく鈍くさい奴だと思っていただろうと思います。今回は、さらに多くのレプリケーションが必要になるわけで、もっと多くの手間と暇がかかることになります。今だったら、もう少し工夫しながら、ずっと早く行うこともできると思いますが、しかし要領よく済ますことにとらわれてしまうと、かえってうまくいかないということも、これまでにさんざん体験してきたので、まあ、トータルで考えれば、それほど違いはなかったのではないかと思います。
このように、例えば、抵抗性と感受性の遺伝子型との間の集団の個体数の変遷について、例えば、感受性の個体数に対する抵抗性の個体数の比の95%信頼区間を設定するときに、1000ブーツトラップ・レプリケーションの分布が必要になるわけですが、1回ずつそれぞれのレプリケーションを吟味しながら分析を進めていく場合、1日に1レプリケーションしかできなければ、3年近くかかってしまうことになります(1000 / 365)。しかし1日に3レプずつ積み上げることができれば、1年かからずに1000レプリケーションを積み上げることができる計算になります。なので、毎日少しずつやれば必ず到達できると信じ、1日3レプずつ増やすことを心がけながら、ほとんど毎日のように、1日かけてブーツトラップ・レプリケーションを増やしていきました。以前のMiyo and Charlesworth(2004)の結果は、170レプリケーションの分布に基づいてブーツトラップ標準誤差の推定をおこないました。今回も、同じデータ・セットを用いてリサンプリングを行い、さらに830レプリケーションを追加して、1000レプリケーションとして95%信頼区間の推定を行うことにしました。これは、もともとのデータ・セットは同じなわけですから、Miyo and Charlesworth(2004)の標準誤差を推定したときの分析の正確さの確認にもなるわけです。このブーツトラップの手順が教科書通りに行われていたならば、ブーツトラップ・レプリケーションの数が170から1000に増加しても、ブーツトラップ・レプリケーションの標準偏差として推定される標準誤差の推定値は、ほとんど変化しないはずなので、それぞれのブーツトラップ・レプリケーションにおいて、もともとのデータ・セットからのリサンプリングがフェアーに行われたことを客観的に示していると言えるのではないかと思います。ブーツトラップ・レプリケーションの数が増加していくにつれて、100日後に感受性の個体数に対する抵抗性の個体数の比(対数変換してある)の標準誤差の推定値がどのように推移していくかを示したグラフ、および1000ブーツトラップ・レプリケーションの分布についてのグラフを以下に示しておきました。これらは、実際にはこれから述べることになる以後の論文の中で用いたグラフです(Miyo [2018]、図3および4)。レプの数が増加しつつあるなかで、ブーツトラップ・レプリケーションの標準偏差として推定される標準誤差はほとんど変化がないこと、そして比率データということで対数変換したブーツトラップ・レプリケーションの分布が正規的であることが明確に示されていると思います。
1レプごとに、コンピューターへの数字の入力、打ち込みにミスがないかどうかなど、そのつどそのつど誤りがないかを嫌になるくらいに見直すことになりました。エジンバラに滞在していた時には、毎日のようにショウジョウバエの死体やショウジョウバエが産んだ卵の数を数えてきましたが、ただ死体の数を数えること、卵の数を数えることがこんなにも大変なことなのだということを、嫌になるほど叩き込まれてきました。研究をやっていると、年をとるにつれて、あれはどうだったか、これはどうだったかと、なかなか先に進めなくなることが多くて嫌になってしまうのですが、1つのレプリケーションを嫌になるほど見直してきたおかげで、この研究については、見直したいと思うことはあまりないのではないかと思います。嫌になるほど見直しをしてきたという自負があるので、以後見直しなどしなくても自信を持つことができるのではないかと思います。手間と暇がかかりましたが、あとあと苦労することがない分、トータルするとあまり変わりがないのではないかと思うのです。
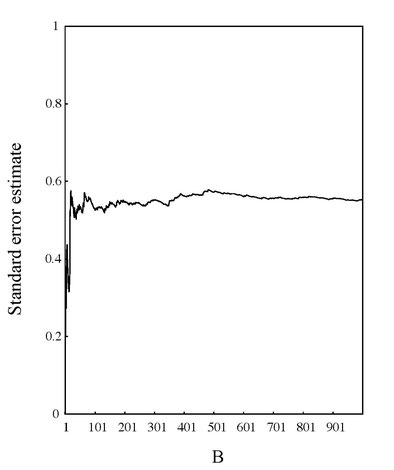
Miyo (2018)の図3より抜粋。1000ブーツトラップ・レプリケーションの標準偏差として推定される標準誤差の推定値の推移。ブーツトラップ・レプリケーションの数が増加しても、ほとんど変化しておらず、教科書どおりにブーツトラップ法が行われていたことが示されていると思います。

Miyo(2018)の図4より抜粋。比率データのため、対数変換した値のブーツトラップ分布(B=1000)。ブーツトラップ・レプリケーションの平均値は-1.6948、観察値に基づく値は-1.6522でした。推定された標準誤差は0.5526であり、観察値に基づく値とブーツトラップ・レプリケーションの平均値との間の差であるバイアスは、-0.0426という結果でした。教科書どおりに分析を行うことができていると判断できると思います。 三代