To illustrate, suppose a rare mutant gene, A, confers resistance in a population where most individuals are homozygous for the susceptible allele (aa). Since allele A is rare, most individuals carrying it are likely heterozygous (Aa), while the number of homozygous (AA) individuals is negligible. When individuals with the Aa genotype mate, their partners are likely to be aa. In other words, if the rare allele A exists in a population dominated by aa, individuals carrying A are typically Aa. Thus, mating primarily occurs between Aa and aa individuals, producing offspring in a 1:1 ratio of Aa to aa. For more detailed calculations, please refer to my book Evolutionary Genetics of Elderly Caring: Why Do We Care for Old Parents? (in Japanese) or the attached diagram. In short, when the allele is rare, the number of Aa genotypes appears to be determined by contributions from fertile Aa individuals. Although they are heterozygous, their frequency can fluctuate as if they were pure homozygotes. Therefore, the model I have pursued since my stay in Edinburgh, which assumes that each genotype reproduces independently, seems sufficient to describe the population state when the resistance gene is a rare dominant allele (effective in the heterozygous state). In fact, in such cases, it has shown strong agreement with other models.
(translated version of the post on December 05, 2021)
例えば、大多数の個体が感受性型の対立遺伝子をホモ接合で保有しているaaの遺伝子型からなる集団に、抵抗性をもたらすまれな突然変異遺伝子Aが生じたとします。このとき、対立遺伝子Aを保有する個体というのは、ほとんどがAaであると考えることができます。なぜならば、対立遺伝子Aはまれなので、それをホモの状態で2個保有している個体はごくわずかであって無視することができるためです。このようなAaの遺伝子型をもつ個体が交配をするときには、その配偶者はaaであると考えることができます。つまり、まれな対立遺伝子Aが、aaで占められている集団に生じた場合、そのまれな遺伝子Aを持つ遺伝子型はAaであり、その交配はAaとaaとの間の交配に注目すればよいことになり、その場合、Aaとaaの子孫が1:1の分離比で産み出されると期待されることになります。ここら辺のより詳細な計算については、拙著『高齢者介護の進化遺伝学 なぜ私たちは年老いた親を介護するのか?』、もしくは添付した図を参照していただきたいのですが、要するに、対立遺伝子がまれであるときに、Aaの遺伝子型の個体数は、見かけ上、繁殖可能なAa遺伝子型からの寄与によって決定され、ヘテロ接合体なのですが、あたかも純粋なホモ接合体であるかのように増加もしくは減少すると考えることができます。よって、私がエジンバラに滞在していたときから追求してきた、それぞれの遺伝子型が単独で増殖しているかのように振る舞うと仮定したモデルは、抵抗性遺伝子がこのようなまれな優性遺伝子である(ヘテロ接合の状態で効果をあらわす)状況では十分に集団の状態を記述することができると考えられます。実際に、そのような状況では、他のモデルととても良い一致が示されています。
(2021年12月5日のポストを再掲)
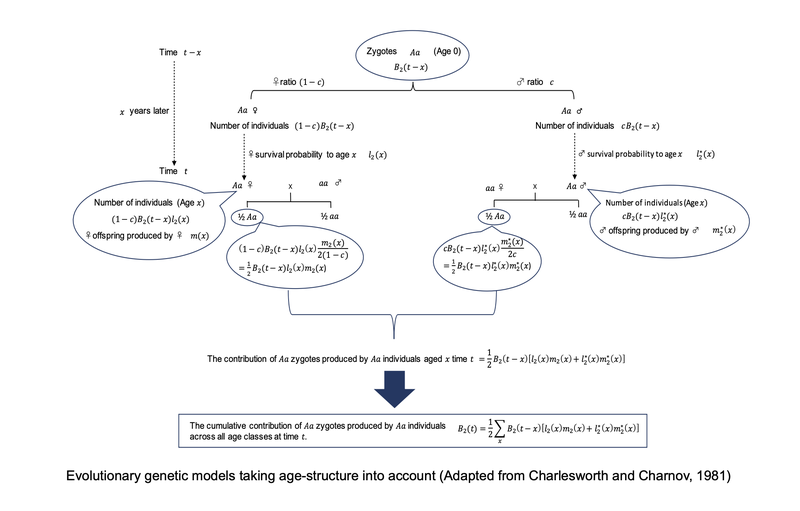
A population model illustrating how a rare mutation behaves in a population already occupied by the other allele. Adapted from Figure 3-2 in my book Evolutionary Genetics of Elderly Caring: Why Do We Care for Old Parents? (in Japanese).
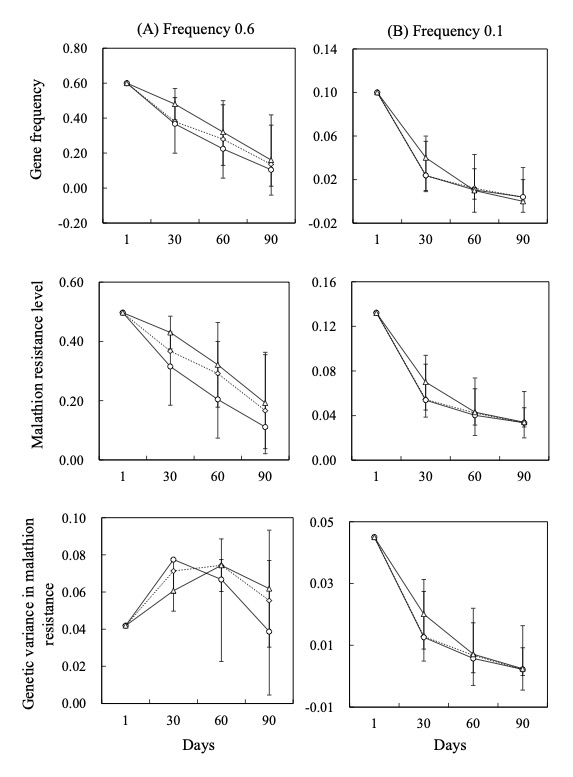
Extracted results from simulation analyses of genetic variation dynamics in malathion resistance, based on different population genetic models. The illustrations show cases where the initial frequency of the resistant-type Ace allele is (A) 0.6 and (B) 0.1. (┅◇┅) represents estimates based on selection equations for gene frequencies (Eq. (3.14) in Charlesworth (1994)), (-△-) represents estimates based on Charlesworth’s approximation method (Eq. (4.11) in Charlesworth (1994)), and (-○-) represents estimates from the population model under density independence, as described here. Error bars for the approximation and the population model indicate 95% confidence intervals for the estimates.